Variação de Coordenadas Equatoriais
Do ponto de vista da astrometria moderna, a Terra é uma plataforma bastante irregular para a observação do céu. A rotação da Terra não é uniforme, seu eixo de rotação não é fixo no espaço e mesmo a forma do planeta e as posições relativas de pontos sobre sua superfície não são fixas. Como resultado, as coordenadas de um objeto no céu, mesmo as equatoriais, não são rigorosamente constantes. Se muda a direção do eixo de rotação, por exemplo, mudam os valores da ascensão reta α e da declinação δ de todos os objetos na esfera celeste. Dependendo da precisão com que desejamos medir a posição das estrelas, faz-se necessária a correção para estes efeitos.
Na antiguidade, medidas astrométricas , ou seja, medidas da posição dos objetos no céu eram feitas com instrumentos rudimentares, sendo portanto de precisão baixa. Assim, os efeitos de que trataremos nesta e, principalmente, na próxima seção não eram muito importantes. Se objetivamos apontar um telescópio com uma precisão de 1", ainda assim não precisamos nos preocupar com variações na forma e superfície da Terra, mas mudanças na orientação do eixo de rotação já se tornam muito importantes. É sobre isso que trataremos neste seção
De certa forma, as coordenadas equatoriais celestes compatibilizam um sistema móvel, baseado na Terra, com um sistema, que seria ideal, fixo com relação às estrelas distantes. Ascensão reta e declinação são bastante análogas à longitude e latitude, usadas para a superfície da Terra. Estes dois sistemas compartilham o mesmo eixo polar e equador, mas a grade de coordenadas celestes não rotaciona junto com o planeta. Graças a esta característica, as coordenadas equatoriais de uma estrela se mantêm constantes ao longo do seu movimento diurno. Contudo, a ascensão reta e declinação verdadeiras não são fixas com relação às estrelas, pois o sistema equatorial, amarrado ao eixo de rotação e ao equador, desloca-se com estes em função de perturbações gravitacionais sofridas pela Terra. Para poder listar as posições das estrelas em catálogos, utilizamos então as coordenadas baseadas na orientação do pólo e do equador em uma época específica. 1° de Janeiro de 1950 e de 2000 (ou seja 1950.0 e 2000.0) são as épocas mais comumente usadas.
Como vimos anteriormente, a origem da ascensão reta se dá em um dos dois pontos onde o Sol, em seu caminho anual por entre as estrelas (eclítica), parece cruzar com o equador celeste. A este ponto chamamos de Ponto Vernal. Em três dimensões, este ponto é a projeção sobre o céu da reta de intersecção entre o plano do equador de Terra e seu plano orbital. Como o primeiro plano é sempre perpendicular ao eixo de rotação e este muda sua orientação constantemente, a posição do Ponto Vernal no céu também muda com relação às estrelas.
Na prática, as coordenadas celestes estão amarradas a objetos observáveis, pois é muito difícil determinar observacionalmente a posição do Ponto Vernal e, por conseguinte, a posição de qualquer astro no céu relativamente a este último. Assim sendo, o sistema de coordenadas associado à época 1950 é definido a partir de posições de estrelas publicadas no quarto Catálogo Fundamental, o FK4, enquanto que o sistema de 2000 é baseado no quinto Catálogo Fundamental, o FK5. Estes catálogos listam estrelas que, em sua maioria, são próximas, de forma que qualquer sistema de coordenadas definida a partir das posições destas estrelas está sujeito a erros causados pelos movimentos dessas estrelas na esfera celeste (movimentos próprios, ver próximo capítulo). Atualmente sabemos que o equinócio obtido a partir do FK4 se desloca com relação ao do FK5 por 0.085" por século.
Atualmente, a definição mais estável de coordenadas para a época 2000 é baseada em 608 radio-fontes extragaláticas que compõem o International Celestial Reference Frame (ICRF). Este sistema de referência é extremamente estável, deslocando-se a menos de 0.020" por século. O ICRF se tornou o sistema de referência fundamental adotado pela União Astronômica Internacional (IAU) em 01/1998.
Por motivos que são em parte históricos e em parte práticos, a variabilidade temporal da direção do eixo de rotação da Terra e da posição de um observador na superfície da Terra com relação a ele são divididos em 4 fatores: precessão, nutação, deslocamento do pólo celeste e deslocamento do pólo . Por definição, precessão e nutação são expressas matematicamente, usando-se equações matemáticas apropriadas. Os outros dois fatores de variabilidade são desvios observados (ou seja, medidos) com relação ao esperado pelas fórmulas matemáticas que descrevem os dois primeiros. Assim sendo, a amplitude destes dois últimos não é previsível para períodos muito longos. Todos os 4 componentes de variabilidade são discutidos com mais detalhe abaixo.
Precessão
Nem o plano orbital da Terra, cuja intersecção com o céu define a eclítica, nem o plano do equador terrestre são fixos com relação a objetos muito distantes, como as fontes extragaláticas do ICRF. O principal movimento é a precessão do eixo de rotação em torno da normal ao plano da órbita (pólo eclítico). Este movimento de precessão é causado por torques gravitacionais devidos à Lua e ao Sol e é chamado de precessão luni-solar. O eixo de rotação da Terra varre um cone no espaço de ângulo de vértice igual a 23.5° uma vez a cada 26.000 anos.
Há ainda a precessão planetária, causada pelas perturbações gravitacionais combinadas dos outros planetas do Sistema Solar. Esta causa uma mudança no plano da órbita da Terra. O pólo eclítico, contudo, se move bem mais lentamente. Se imaginarmos seu movimento com relação às fontes extragaláticas, o eixo de rotação muda de posição a uma taxa de 50" por ano, enquanto que a normal ao plano da órbita varre apenas 0.5" no céu. Ambos os movimentos combinados formam o que chamamos de precessão geral. Há desvios com relação à precessão geral, de curto período, que também são previsíveis e expressos por fórmulas matemáticas, aos quais chamamos de nutação, que será discutida na próxima seção.
Equações para o efeito da precessão, de precisão da ordem de 1", sobre as coordenadas equatoriais são dadas abaixo. Elas se aplicam para qualquer data dentro de um intervalo de uns 20 anos, centrado no ano 2000.
dδ / dt = n cos α
dα / dt = m + n sen α tan δ
onde m=3.07419 s/ano e n=20.0383 "/ano ou 1.33589s/ano. Estes valores, como já mencionado, são válidos por uns 20 anos, centrados no ano 2000. A variação das coordenadas equatoriais ascensão reta (α) e declinação (δ) são expressas em segundos de tempo e segundos de arco, respectivamente.
As fórmulas, como as acima, para calcular as correções sobre as coordenadas equatoriais de um astro em diferentes épocas e para intervalos de tempo, são dadas pelo Astronomical Almanac. Essas fórmulas são muito úteis, pois os catálogos astronômicos geralmente listam as coordenadas das estrelas para uma época arredondada, como 1950.0 ou 2000.0. Se quisermos localizar com precisão um objeto no céu em uma época arbitrária, teremos necessariamente que corrigir as coordenadas catalogadas para a precessão.
Vemos pelas fórmulas acima que a precessão do eixo é muito lenta. De maneira aproximada, a variação de α é da ordem de 3s por ano e a de δ de uns 20"/ano. A figura abaixo mostra a variação da posição dos pólos celestes devida à precessão. A figura da esquerda mostra a situação no presente, em que o pólo norte celeste coincide aproximadamente com a estrela Polaris. Daqui a milhares de anos, o mesmo pólo celeste coindirá aproximadamente com a estrela Vega (figura da direita).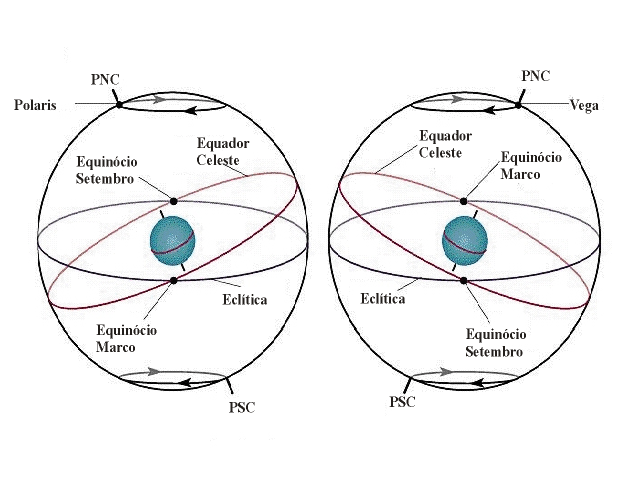
Segue um exemplo de como calcular as correções para o efeito da precessão usando a fórmula dada acima e que repetimos abaixo:
dδ / dt = n cos α
dα / dt = m + n sen α tan δ
Computemos a precessão do núcleo da Galáxia de Andrômeda durante 10 anos, conhecidas suas coordenadas equatoriais no ano 2000.
α(2000)=00hr 42m 44.32s; δ(2000)= +41°16'08.5"
O primeiro passo é converter ambas para graus decimais:
Cálculo da precessão:
Para computar as coordenadas para o ano 2010, essas correções devem ser adicionadas às coordenadas do ano 2000.
Nutação
Movimentos previsíveis do eixo de rotação terrestre em escalas de tempo (períodos) de 300 anos ou menos são combinados para formar o que chamamos de nutação. Esta pode ser tomada como uma correção de primeira ordem à precessão. De acordo com o modelo de nutação mais atual, este efeito é composto de 106 termos harmônicos envolvendo senos e cossenos com diferentes freqüências, em sua maioria efeitos secundários de torque gravitacional do Sol e da Lua, mais 85 correções devidas a efeitos planetários. Os principais termos de nutação são: um termo de período igual a 18.6 anos (período de precessão da órbita da Lua), um termo de 182.6 dias (meio ano), um outro de 13.7 dias (meio mês) e um de 9.3 anos (período de rotação do perigeu lunar).
As correções para nutação dadas abaixo têm uma precisão da ordem de 1".
Δα = (cosε + senε sinα tanδ) dλ - cosα tanδ dε Δδ = senε cosα dλ + sinα dε
onde Δα e Δδ são adicionadas às coordenadas médias (já corrigidas para precessão), resultando nas chamadas coordenadas aparentes (ou verdadeiras). Na expressão acima, ε é a obliquidade da eclítica, cujo valor pode ser obtido, dia a dia, no Astronomical Almanac. Os termos de nutação em longitude eclítica (dλ) e obliqüidade eclítica (dε), respectivamente, são também encontrados em anuários como o Astronomical Almanac, ou calculados a partir da teoria de nutação, levando-se em conta os dois termos dominantes.
dλ = -17.3 * sin(105.7 - 0.05295 * d) - 1.4 * sin(199.5 + 1.97129 * d) dε = 9.4 * cos(105.7 - 0.05295 * d) + 0.7 * cos(199.5 + 1.97129 * d)
onde d = Data Juliana - 2451909.5, os argumentos do seno e do cosseno sendo expressos em graus, e dλ e dε em segundos de arco.
Exemplo de tabela do Anuário do ON listando os termos de nutação.
Os coeficientes que multiplicam dλ e dε, e que dependem somente das coordenadas equatoriais da estrela, podem ser encontrados no Apparent Places of Stars:
Exemplo de tabela com os coeficientes úteis para a correção para nutação
Para ajudar a visualizar em separado os efeitos da precessão e da nutação podemos fazer uso da figura abaixo. Nela, vemos a posição da Terra (T), a direção do pólo da eclítica, PE, e a direção do pólo celeste, ou seja, do eixo de rotação (PC) em duas épocas diferentes. A variação no espaço da direção do eixo de rotação da Terra sem alterar-se a obliquidade da eclítica é a precessão luni-solar, representada pelo cone maior da figura. Superposto a este há um cone menor, que representa a variação ondular do eixo causada pela nutação.

Deslocamento do Pólo Celeste
Este efeito é a parte imprevisível da nutação. Os valores desse efeito são publicados pelo IERS Bulletin A com componentes em separado em longitude (dλ) e obliqüidade (dε).
Movimento do Pólo
Devido a movimentos internos e deformações na forma da Terra, uma linha que interliga as posições de diferentes observadores na sua superfície não é fixa com relação ao eixo de rotação. A variação na posição relativa de um observador com relação a este eixo é o que chamamos de movimento do pólo. Para um observador qualquer, este movimento tem o efeito de mudar sua latitude e sua longitude, que por seu turno é necessária nas transformação de coordenadas terrestres para celestes. O International Earth Rotation Service (IERS) define um sistema de referência terrestre baseado em um eixo de referência, chamado de IERS Reference Pole (IRP) . As fórmulas abaixo nos dão a variação de latitude, longitude e do azimute de uma mira em função dos valores médios das próprias coordenadas (φmed, λmed) e das coordenadas desse pólo médio expressas em um sistema cartesiano, (x,y).
Δφ = φmed - φobs = x cosλ + y senλ
Δλ = λmed - λobs = -(x senλ + y cosλ) tgφ
ΔA = Amed - Aobs = -(x senλ + y senλ) secφ
O componente dominante do movimento do pólo, chamado de oscilação de Chandler, é um movimento aproximadamente circular do pólo de referência em torno do pólo celeste, de amplitude de cerca de 0.7" e um período de uns 14 meses aproximadamente. Irregularidades em escalas de tempo mais curtas e também mais longas, devidas a movimentos no interior do planeta, são imprevisíveis e tem que ser monitoradas por observações. A soma do componente de Chandler com os componentes irregulares são publicados semanalmente no IERS Bulletin A, juntamente com previsões para vários meses de antecipação
Basilio Santiago, santiago@if.ufrgs.br
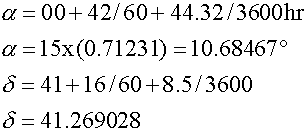
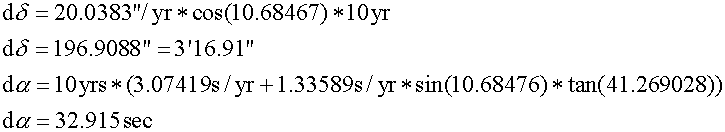
Nenhum comentário:
Postar um comentário